In diesem Artikel erkläre ich dir die 9 Schritte, die du durchlaufen musst, um eine ANOVA für Gruppenvergleiche korrekt zu berechnen und zu berichten. 

Bevor es losgeht: Die ANOVA für Gruppenvergleiche wird auch Zwischensubjekt-ANOVA oder Between-Subjects-ANOVA genannt. Du verwendest sie immer dann, wenn deine Patienten unterschiedlichen Gruppen angehören und keine Messwiederholung vorliegt. Ist dies bei dir nicht der Fall, dann lies noch einmal Teil 1 dieser Artikelserie und identifiziere den richtigen ANOVA-Typ für dein Studiendesign.

Unser Studienbeispiel:

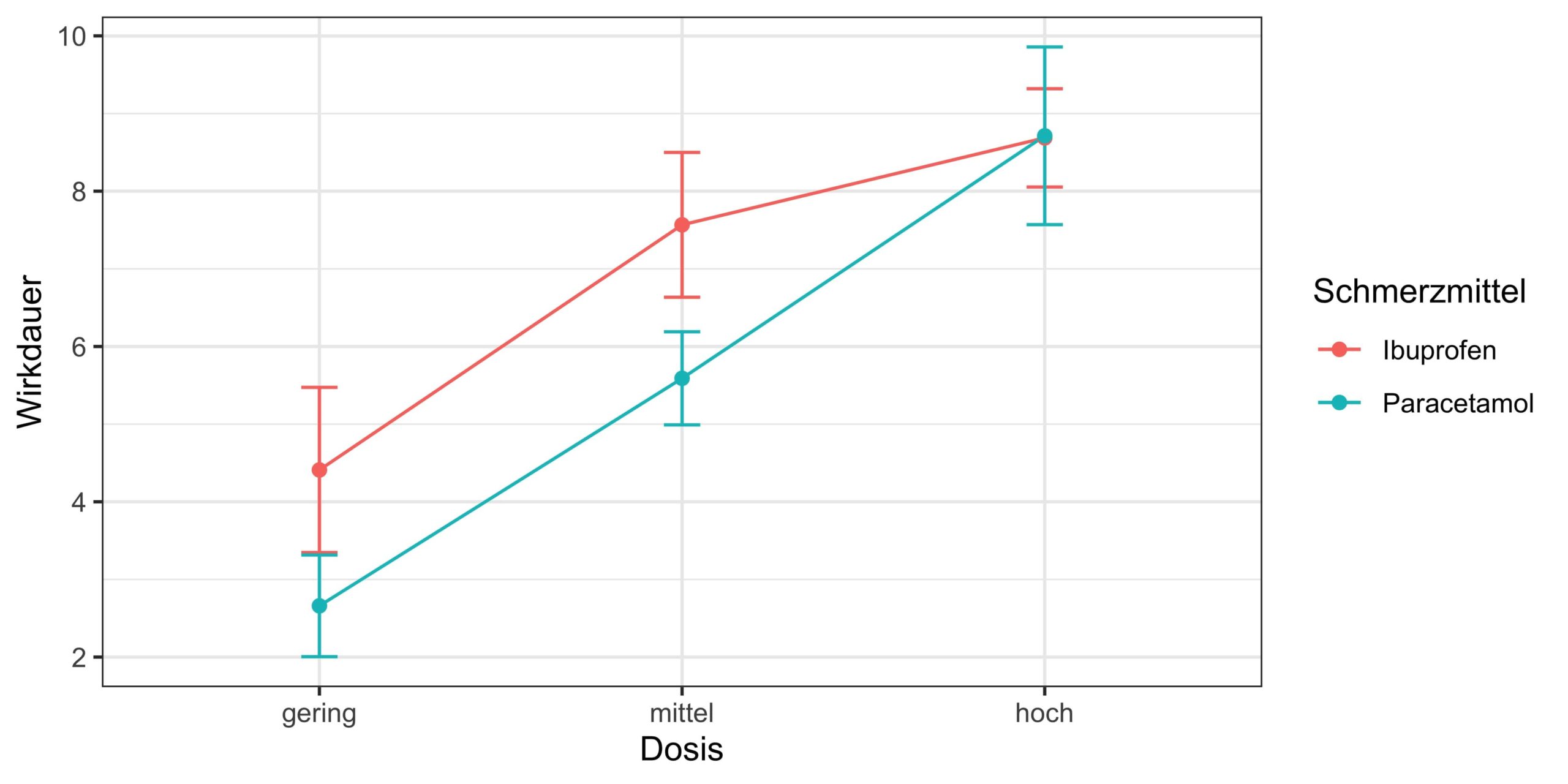
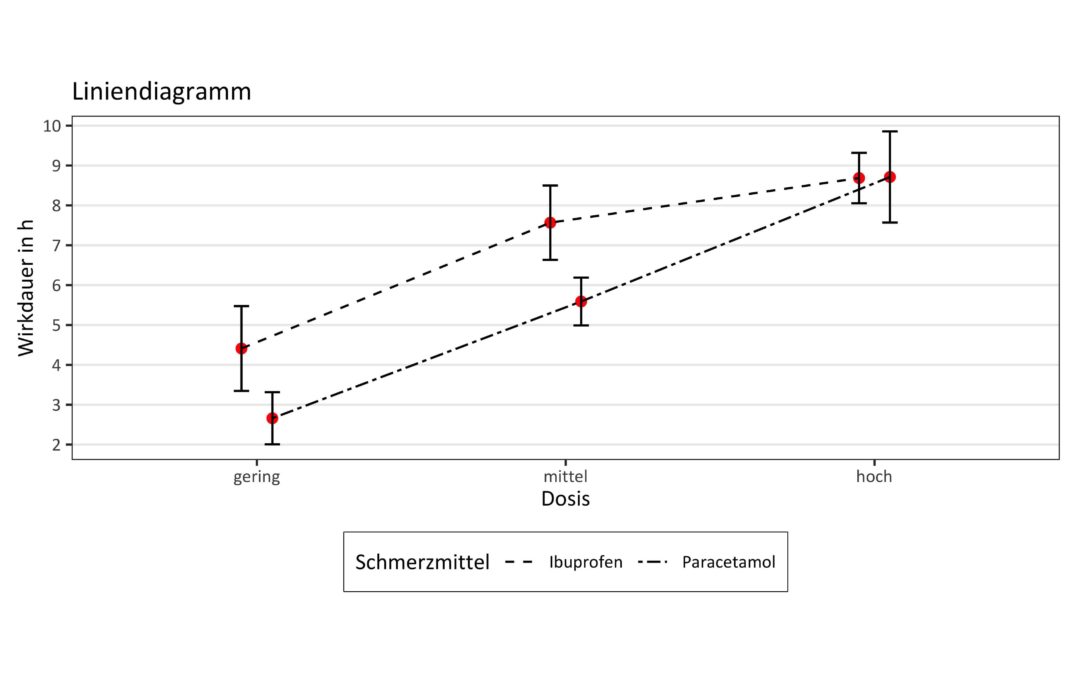
Nehmen wir noch mal unser hypothetisches Beispiel aus dem ersten Teil unserer Artikelserie zu ANOVA. Wir möchten testen, ob sich die Schmerzmittel Paracetamol und Ibuprofen bzgl. ihrer Wirkdauer unterscheiden. Aber nicht nur das. Wir möchten ebenfalls testen, ob die gegebene Dosis (hoch, mittel, niedrig) einen Einfluss auf die Wirkdauer besitzt. Aber am allermeisten interessiert uns, ob der Effekt der Dosis vielleicht sogar unterschiedlich ist, je nachdem welches Schmerzmittel gegeben wurde.

Dafür bilden wir 6 verschiedene Patientengruppen, die jeweils eines der beiden Medikamente bekommt und eine der drei Dosierungen. Jeder Patient kommt also genau einmal innerhalb der Studie vor.

Aus diesen 2 Faktoren resultieren verschiedene Effekttypen, die ich dir in Teil 1 dieser Artikelserie genau erklärt habe. Dort habe ich auch alle Begriffe erläutert. Hast du diesen Artikel also noch nicht gelesen, würde ich dir empfehlen, damit zu starten.

Schritt 1 – Die Vorbereitung deines Datenfiles

Schritt 1 ist immer der bedeutenste: Wir bringen Ordnung in dein Datenfile. Das ist immens wichtig, da jedes statistische Verfahren spezielle Anforderungen an das zugrundeliegende Datenfile stellt. Ist diese Ordnung falsch, funktioniert die Analyse nicht.

Die ANOVA für Gruppenvergleiche erfordert eine ID-Variable, sowie für jeden Faktor eine weitere Variable, die für jeden Patienten die ihm zugeordnete Faktorstufe enthält. Hier würdest du z.B. für den Faktor Medikament für jeden Patienten eintragen, ob er Paracetamol oder Ibuprofen erhalten hat. Für die Dosierung würdest du eintragen ob der Patient eine hohe, mittlere oder niedrige Dosierung bekommen hat.

Weiterhin benötigst du eine Variable, die die abhängige Variable enthält, also die beim Patienten gemessene Angabe zur Wirkdauer. Hast du das erledigt, ist dein Datenfile fertig.

↑ Zurück zur Übersicht

Schritt 2 – Deskriptive Statistik

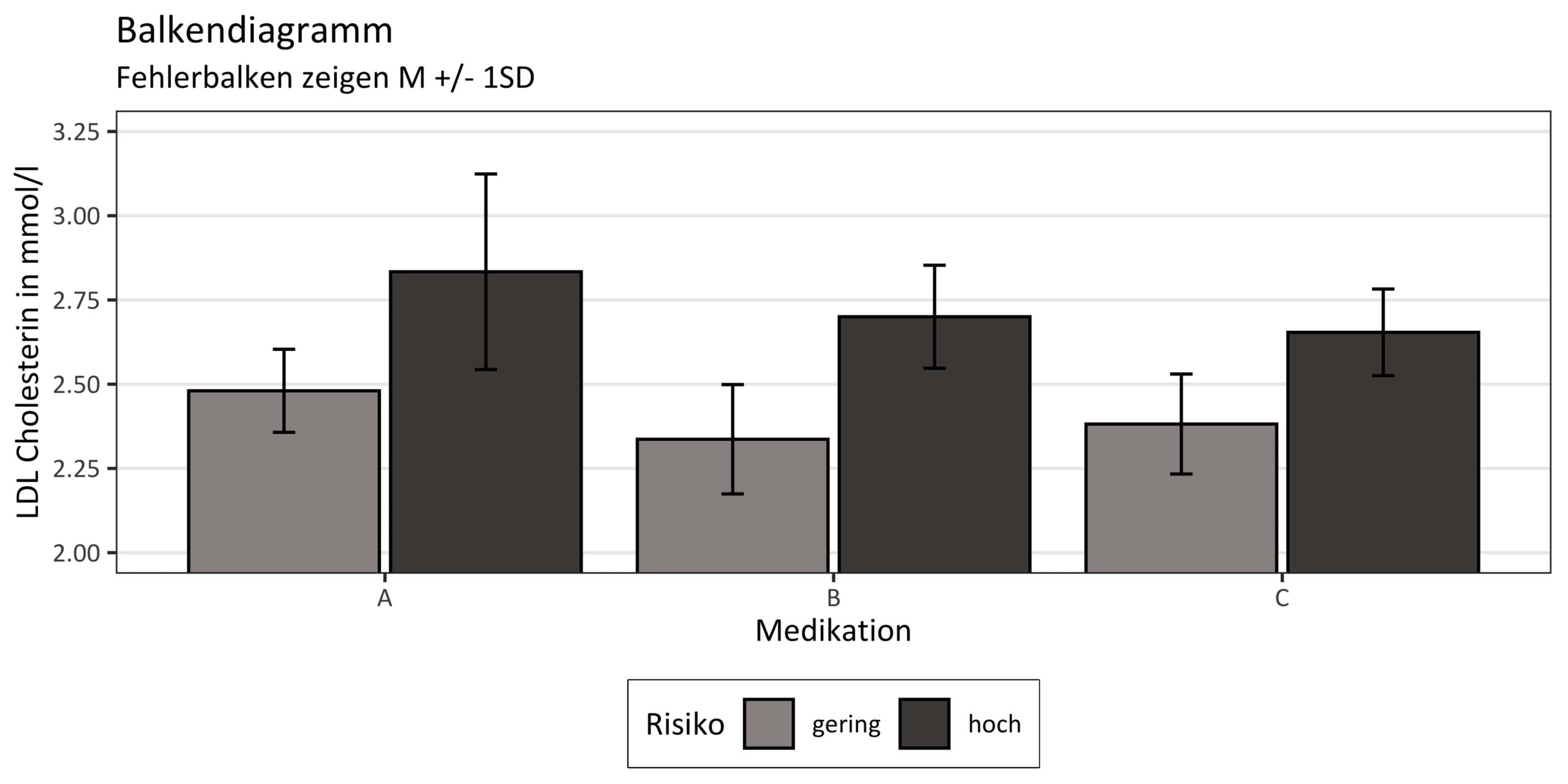
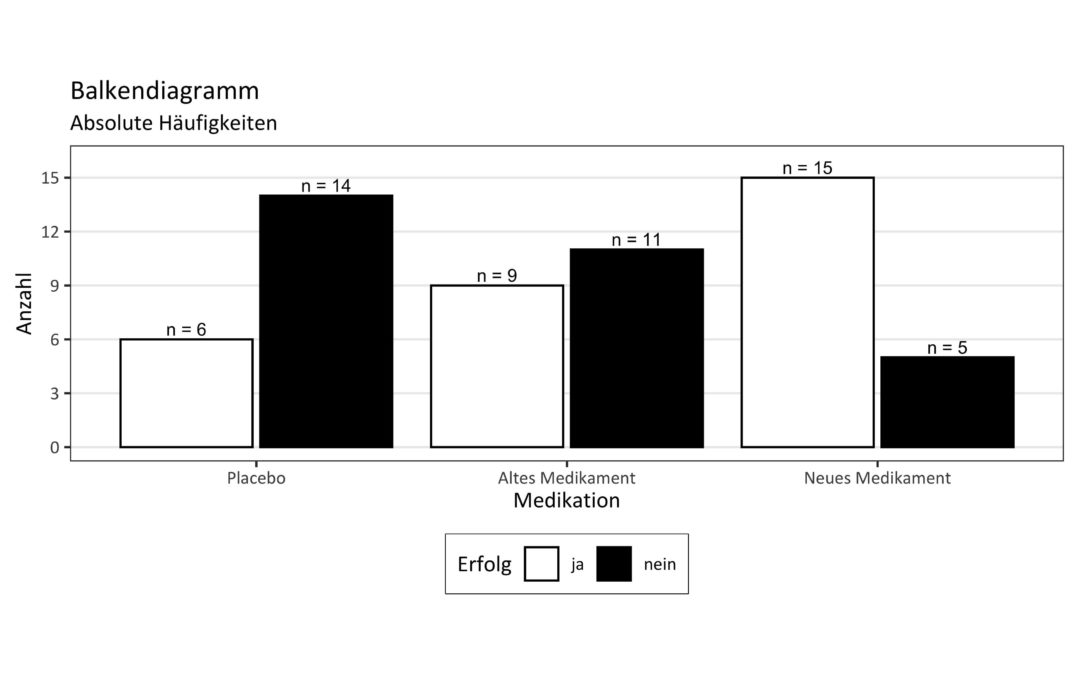
Es ist immer gut einen Überblick über die eigenen Daten zu bekommen. Daher solltest du in Schritt 2 eine deskriptive Statistik mit Mittelwerten und Standardabweichungen für jede Gruppe innerhalb deiner Daten erstellen. Prüfe außerdem, ob dein Datensatz Ausreißer enthält. Falls ja, solltest du übelegen, was dahintersteckt. Sind Messfehler enthalten, oder ist dein Patient wirklich so krank, schwer oder groß? Weiterhin solltest du dir eine Grafik über alle Faktorstufen erstellen, damit du schon mal grob siehst, wie die Effekte aussehen. 

Schritt 3 – Berechnung der ANOVA für Gruppenvergleiche

In Schritt 3 berechnest du die ANOVA nun erstmals ganz konkret. Du bekommst dabei 3 Effekte: die Haupteffekte Schmerzmittel und Dosis, und den Interaktionseffekt, der beide Faktoren kombiniert. Was diese Effekte bedeuten und welche der wichtigste ist, erklären wir dir in Teil 1 dieser Artikelserie.

Die Berechnung der ANOVA erfolgt je nach verwendeter Software unterschiedlich. Wir berechnen sie in diesem Beispiel in R mit dem Paket aov (). Das ist ganz einfach, besonders, wenn man wie wir hier, automatische Vorlagen verwendet, in die man einfach nur seine Variablennamen eintippen muss. Wie das geht zeigen wir dir in unserem ANOVA-Kurs für Gruppenvergleiche, der dich Schritt-für-Schritt durch die ANOVA führt bis hin zu Vorlagen für deinen ANOVA-Bericht im Ergebnis- und Methodenteil. Da dir unser Kurs alle Arbeit abnimmt, gehen wir hier nicht auf die Einzelheiten des R-Codes ein.

↑ Zurück zur Übersicht

Schritt 4 – Prüfen der Annahmen

Nachdem du die ANOVA berechnest hast, prüfst du im nächsten Schritt, ob du sie überhaupt rechnen durften. Dieses Vorgehen ist zwar falsch herum, aber tatsächlich funktioniert das Prüfen der Annahmen der ANOVA viel besser, wenn man sie schon gerechnet hat. Und wir wollen doch so effizient wie möglich vorgehen, oder?

Hier sind folgende Kriterien wichtig:

1. Sind unsere Daten normalverteilt?

Um das zu beurteilen, kannst du QQ-Plots und den Shapiro-Wilk-Test nutzen (weiteratmen, mit unserem Kurs machst du das in 2 Minuten).

2. Liegt eine Varianzhomogenität vor?

Das sagt uns der Levene‘s Test, ist er nicht signifikant ist alles gut.

Hier teilt sich nun die Analyse in zwei Ströme auf, die aber vom Prinzip her sehr ähnlich sind.

Werden die Annahmen der ANOVA erfüllt oder sind deine Gruppen sehr groß (N > 30 pro Untergruppenkombination), dann darfst du einfach normal weitermachen und die Ergebnisse der parametrischen ANOVA aus Schritt 3 interpretieren.

Gibt es in deinem Datensatz ernsthafte Probleme, müsstest du nun eigentlich auf das nicht-parametrische ANOVA-Äquivalent, dem Kruskal-Wallis-Test ausweichen. Der hat aber leider nicht die Möglichkeit Interaktionen zu testen und das wollen wir ja eigentlich.

Daher haben wir dir in unserem ANOVA-Kurs ein Skript geschrieben, dass dir erlaubt, die bisherige ANOVA einfach weiter zu verwenden, allerdings überführen wir sie nun in eine robuste Form. Das heißt, wir machen sie unempfindlich gegenüber gravierender Annahmeverletzungen (das ist wirklich cool und viel eleganter als eine nicht-parametrische ANOVA).

Dafür bauen wir in die ANOVA ein sogenanntes Bootstrapping-Verfahren ein, dass mit Hilfe von 2000 Stichproben mit Zurücklegen eine robuste Teststatistik errechnet, aus der dann wiederum ein robuster p-Wert und eine robuste Effektstärke abgeleitet wird.

Was du dir hier nur merken musst ist, dass du weiterhin eine relativ normaldesignte ANOVA rechnen kannst, die wir aber unempfindlich auf mögliche Annahmeverletzungen gemacht haben.

Einen Code zu schreiben, der das kann und den du total einfach an deine Studie anpassen kannst, hat meinen R-Spezialisten Simon ziemlich viel Zeit und Nerven gekostet, aber ich finde es hat sich gelohnt!

↑ Zurück zur Übersicht

Schritt 5 – Effekte untersuchen

Egal welche ANOVA du gerechnet hast, die Ergebnisse liegen vor. Nun kannst du anhand der Signifikanzen entscheiden, welchen Effekt du weiter untersuchen möchtest: die Interaktion oder eine oder beide Haupteffekte? Die Antwort findest du im ersten Teil des Artikels – nur soviel – ist die Interaktion signifikant, kannst du die Haupteffekte ignorieren.

Hast du vorher eine parametrische ANOVA (also die ganz normale) gerechnet, machst du nun mit den t-Tests weiter, um deine Effekte zu verstehen. An dieser Stelle solltest du ggf für multiple Vergleiche korrigieren. Dabei gibt es verschiedene Methoden, wie z.B. die Bonferroni- oder die Holm-Korrektur, die unterschiedlich streng sind.

Je nachdem welche Effekte dich interessieren, kannst du dabei unterschiedlich vorgehen. In unserem Kurs zeigen wir dir genau wie das geht.

Hast du dich vorab für eine robuste ANOVA entschieden, machst du mit YUEN-Tests weiter, die ebenfalls robust sind und für multiples Testen korrigiert wurden.

Und da nicht nur die Signfikanz eines Tests wichtig ist, sondern auch die Stärke des Effekts (die sich übrigens nicht allein an der Signfikanz festmachen lässt), solltest du nun noch Effektstärken berechnen. In unseren Vorlagen erledigen wir das gleich automatisch mit, genau wie die dazugehörigen Konfidenzintervalle, die du benötigst, sobald es in Richtung einer Publikation gehen soll. 

 Schritt 6 – Geplante Kontraste

Hattest du vorab feste Hypothesen definiert, solltest du über eine elegante Alternative zu t-Tests nachdenken – die geplanten Kontraste. Geplante Kontrast ersetzen innerhalb eines Rechenschritts viele einzelne t-Tests und sind daher sehr praktisch.

Allerdings kann es ein bisschen schwierig sein sie anzulegen, in unserem Kurs haben wir daher viele verschiedene geplante Kontraste für dich entworfen, so kannst du direkt loslegen:

Wähle einfach einen Kontrast aus, der deine Hypothese widerspiegelt und schon bist du fertig mit deiner Datenanalyse.

↑ Zurück zur Übersicht

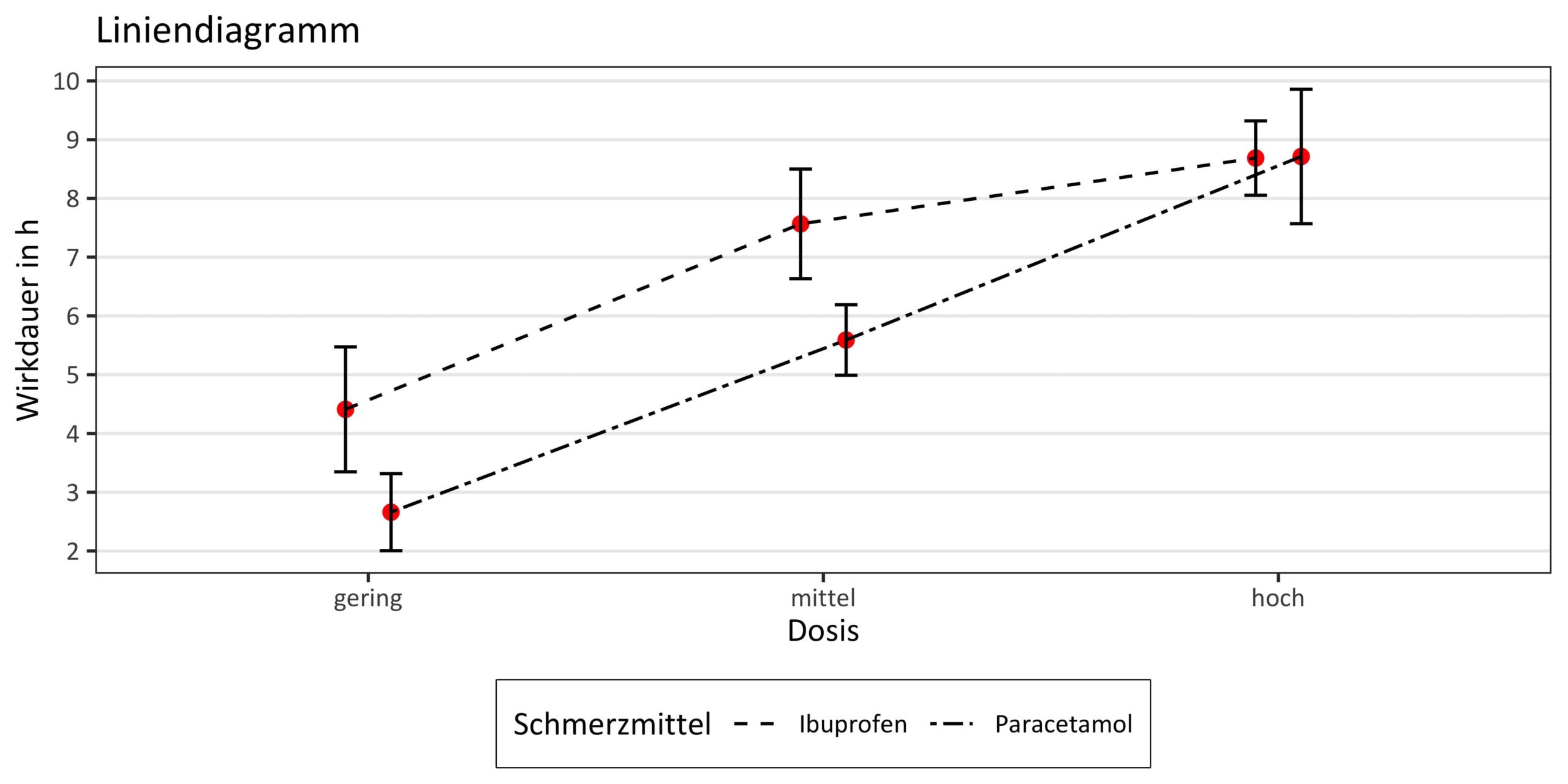
Schritt 7 – Grafik erstellen

Keine Statistik ohne schicke Grafik. Natürlich hast du schon deine Grafik aus Schritt 1, aber für eine Dissertation oder Publikation muss mehr her. Daher solltest du dir noch einmal genug Zeit nehmen, deine Grafik aufzuhübschen. Verwendest du unseren Kurs, kannst du das direkt mit Hilfe unseres letzten Skripts ratz fatz erledigen. Wir haben dabei extra darauf geachtet, dass du sie sowohl für deine Dissertation als auch für eine mögliche Publikation verwenden kannst und alle notwendigen Anforderungen erfüllt sind. 

Schritt 8 – Berichte die ANOVA im Methoden- & Ergebnisteil

Jetzt kommen wir zum finalen Teil, dem Berichten der ANOVA für Gruppenvergleiche im Ergebnis- und Methodenteil.

Hier gehst du folgendermaßen vor:

Methodenteil:

Zuerst beschreibst du im Methodenteil genau, welche Art der ANOVA du gerechnet hast, wie du dabei vorgegangen bist, welche Parameter du später wofür im Ergebnisteil berichten wirst und wie diese einzuordnen sind.

Für die ANOVA für Gruppenvergleiche aus unserem Beispiel würdest du beispielsweise berichten, dass du eine Zwischensubjekt-ANOVA mit den Faktoren Schmerzmittel (Ibuprofen vs. Paracetamol) und Dosis (hoch, mittel, niedrig) bzgl. ihrer Auswirkung auf die abhängige Variable Wirkdauer getestet hast.

Du solltest ebenfalls nennen, dass dies in den Haupteffekten Schmerzmittel und Dosis, sowie der Interaktion Schmerzmittel x Dosis resultierte. Weiterhin solltest du nennen, dass du im Falle einer signifikanten Interaktion diese mit Hilfe von post-hoc t-Tests weiter ausdifferenziert hast, und signifikante Haupteffekte nur dann weiter untersucht hast, falls die Interaktion nicht signifikant wurde. Verwendest du geplante Kontraste anstelle der t-Tests kannst du dies alternativ berichten.

Nenne auch, dass du die Annahmen der ANOVA geprüft hast und ob und wie du vorgegangen bist, falls die Annahmen nicht erfüllt wurden. In unserem Beispiel könntest du berichten, dass du eine robuste ANOVA berechnet hast, die mit Hilfe von Bootstrapping über 2000 Stichproben eine robuste Teststatistik ermittelt hat und die gefundenen Effekte anhand von Yuen-Tests weiter untersucht wurden.

Am Schluss solltest du aufzählen, welche Effektstärken du berechnet hast und wie diese zu interpretieren sind. Gib dazu Werte an, die vermitteln, was für die jeweilige Effektstärke ein kleiner Effekt, ein mittlerer Effekt und ein großer Effekt ist. Dies hilft dem Leser, deine Ergebnisse später zu bewerten.

Auf diese Weise hat dein Leser die Möglichkeit, dein Vorgehen genau nachzuvollziehen.

Ergebnisteil:

Im Ergebnisteil berichtest du nun die Ergebnisse der ANOVA. Schreib hier auf keinen Fall noch einmal über dein statistisches Vorgehen, das gehört in den Methodenteil. Berichte ausschließlich, was die ANOVA ergeben hat.

In unserem Beispiel würdest du berichten, dass sich innerhalb der ANOVA eine signifikante Interaktion Schmerzmittel x Dosis ergeben hat, die im Rahmen der post-hoc Testung ergab, dass die Wirkdauer beider Schmerzmittel mit steigender Dosis anstieg. Hierbei zeigte sich allerdings, dass dieser Anstieg für Ibuprofen von der mittleren zur hohen Dosis weniger stark ausfiel als für Paracetamol, sodass die signifikant höhere Wirkdauer von Ibuprofen im Vergleich zu Paracetamol, die in der niedrigen und mittleren Dosis zu finden war, in der hohen Dosis verschwand.

Folgendes solltest du beachten:

• Berichte sowohl die statistischen Kennwerte der Interaktion, als auch alle relevanten post-hoc Tests samt Effektstärken.
• Konzentriere dich inhaltlich auf die Effekte, die dich wirklich interessieren. Es ist nicht unbedingt notwendig jeden Untertest zu berichten. Belege dabei jede wertende Aussage mit einem dazugehörigen (signifikanten) Tests.
• Berichte auch immer wieder deskriptive Statistiken, damit der Leser die wirkliche klinische Bedeutung der Effekte erkennen kann.
• Berichte deine Ergebnisse objektiv, diskutieren und klinisch bewerten darfst du sie hier noch nicht. Das erfolgt in der Diskussion.

Wie du siehst, ist der Ergebnisteil eine recht objektive Sache, bei der du deine Resultate relativ neutral berichten solltest. Das kann manchmal langweilig wirken, ist aber notwendig, um die Grundordnung des wissenschaftlichen Schreibens einzuhalten.

↑ Zurück zur Übersicht

Schritt 9 – Die klinische Bewertung deiner Effekte

Prinzipiell hast du nun alles statistisch relevante erledigt – aber meiner Meinung nach fehlt noch das Wichtigste: Du musst deine Effekte noch klinisch interpretieren und bewerten. Das liegt daran, dass statistische Effekte Systematiken ausdrücken, die dir helfen sollen, abzuschätzen, ob deine gefundenen Ergebnisse verlässlich sind oder nur zufällig.

Die statistische Bedeutung eines Effekts ist somit nur die eine Seite der Medaille – die zweite ist die klinische Bedeutsamkeit des Effekts, dessen Bewertung du niemals vergessen solltest. Es kann z. B. sein, dass du hochsignifikante Effekte mit großen Effektstärken hast, die ermittelten Gruppenunterschiede aber minimal sind.

Welche klinische Relevanz hätte z. B. ein hochsignifikanter Haupteffekt Schmerzmittel, der dir anzeigt, dass Ibuprofen im Mittel  3 Minuten länger wirkt als Paracetamol? Genau, so gut wie keine.

Du solltest deine Effekte also immer anhand der deskriptiven Statistik klinisch einordnen. Diese klinische Bewertung erfolgt dabei nicht im Ergebnisteil, sondern erst später in der Diskussion. Im Ergebnisteil konzentrierst du dich einzig und allein darauf, deine Effekte objektiv zu berichten.

Hast du alle Schritte durchlaufen, hast du die ANOVA gemeistert:

Vom Aufbau des Datenfiles bis zur kritischen Einordnung der Ergebnisse.

Herzlichen Glückwunsch!

↑ Zurück zur Übersicht