Zusammenhänge verstehen: Die Korrelationsanalyse in der medizinischen Statistik
Zusammenhänge verstehen: Die Korrelationsanalyse in der medizinischen Statistik
- Warum werden in der medizinischen Statistik eigentlich so häufig Korrelationen berechnet? Und was genau ist eine Korrelation?
- Kann man Korrelationen immer berechnen? Und was sollte man bei der Berechnung und Interpretation von Korrelationen beachten?
- Was sind Scheinkorrelationen und verdeckte Korrelationen?
- Und warum sind Korrelation und Kausalität nicht das Gleiche?
In diesem Artikel werden wir diese Fragen beantworten (und noch viel mehr!), ohne dass du dafür tiefere statistische Kenntnisse benötigst.
Aber zunächst noch ein Hinweis, bevor es losgeht:
Wenn man in der Statistik von „der Korrelation“ spricht, meint man in der Regel die Korrelation nach Pearson (kurz: Pearson-Korrelation oder auch Produkt-Moment-Korrelation). Es gibt allerdings auch für spezielle (und deutlich seltenere) Fälle andere Korrelationsarten, die man berechnen kann. Wir werden diese Fälle ganz am Schluss dieses Artikels behandeln. Bis dahin ist mit „Korrelation“ immer die Pearson-Korrelation gemeint.
Ganz wichtig:
Um die Pearson-Korrelation zwischen zwei Merkmalen sinnvoll berechnen zu können, sollten beide Variablen mindestens intervallskaliert sein.
Zusammenhang und linearer Zusammenhang
In der medizinischen Statistik findet man häufig Untersuchungsfragen der Art „Gibt es einen Zusammenhang zwischen der Dosis von Medikament X und der Herzfrequenz (oder der Stärke von Kopfschmerzen, der Dauer einer Infektion, oder, oder, oder)?“
Eine (!) Möglichkeit, Fragen dieser Art nachzugehen, ist die Korrelationsanalyse. Der Knackpunkt solcher Fragestellungen ist, dass das Wort „Zusammenhang“ aus statistischer Perspektive ziemlich viele Bedeutungen haben kann. Mit einer Korrelationsanalyse untersucht man allerdings nur eine ganz bestimmte Form des Zusammenhangs, nämlich den linearen Zusammenhang zwischen zwei Variablen. Ganz allgemein dient die Korrelation dazu, die Stärke des linearen Zusammenhangs zwischen zwei Merkmalen zu quantifizieren, also in einer Zahl auszudrücken.
Aber was genau ist ein linearer Zusammenhang? Das wollen wir dir gleich an einem einfachen Beispiel erklären.
Angenommen, du möchtest den Zusammenhang zwischen der Dosis eines Medikaments und der Herzfrequenz untersuchen. Du erhebst dazu nun bei 100 Personen beide Merkmale und schaust dir die erhobenen Daten anschließend anhand eines Streudiagramms (einer Punktwolke) an. Du solltest dir übrigens immer, wenn es um die Analyse von Zusammenhängen zwischen zwei Variablen geht, deine Daten grafisch veranschaulichen. Warum du das tun solltest, wird gleich deutlich werden.
Die folgende Grafik zeigt dir sechs mögliche (und natürlich vollkommen fiktive) Punktwolken, die man für dieses Beispiel bekommen könnte. Es gibt natürlich noch unzählige andere Möglichkeiten, wie die Punktwolke aussehen könnte.
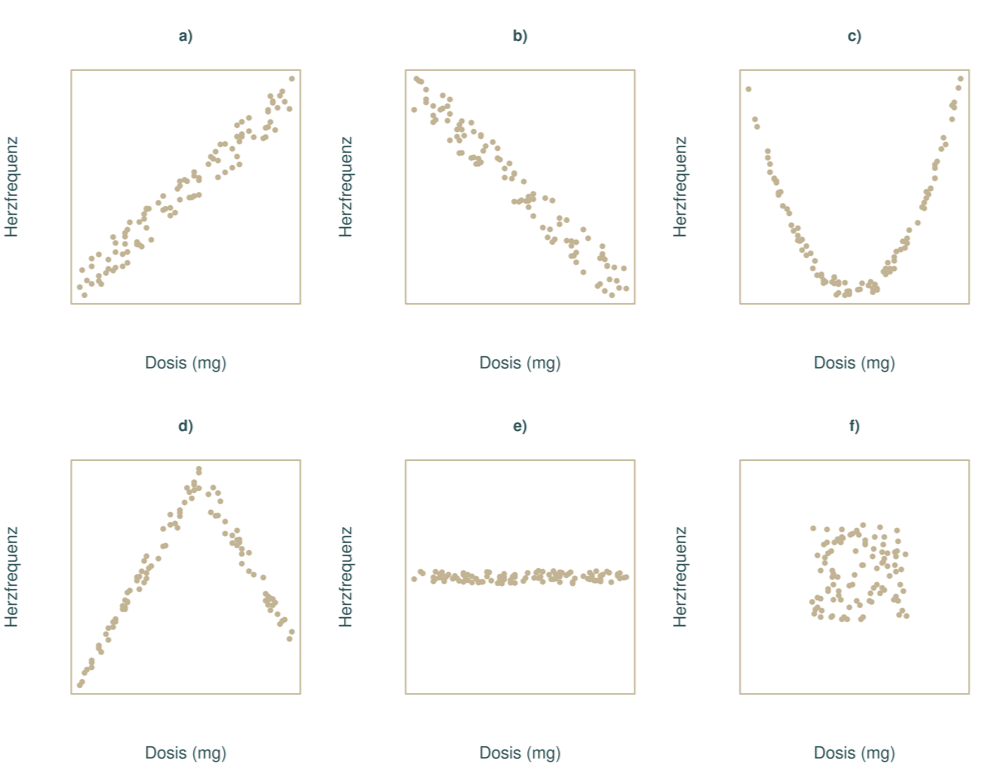
Ohne große statistische Kenntnisse zu haben, könnte man die Punktwolken nun folgendermaßen beschreiben:
Fall a) Hier lässt sich ein deutlicher Zusammenhang erkennen. Mit einer höheren Dosis geht tendenziell auch eine höhere Herzfrequenz einher. Man spricht hier auch von einem positiven linearen Zusammenhang („je mehr von dem einen, desto mehr von dem anderen“).
Fall b) Hier lässt sich ebenfalls ein deutlicher Zusammenhang erkennen. Mit einer höheren Dosis geht hier jedoch tendenziell eine niedrigere Herzfrequenz einher. Man spricht hier auch von einem negativen linearen Zusammenhang („je mehr von dem einen, desto weniger von dem anderen“).
Fall c) Hier lässt sich ebenfalls ein deutlicher Zusammenhang erkennen. Der Zusammenhang ist hier allerdings nicht linear, sondern „komplexer“. Man nennt das manchmal auch einen „U-förmigen“ oder auch quadratischen Zusammenhang. Inhaltlich bedeutet das hier, dass mit niedrigeren Dosen eine höhere Herzfrequenz einhergeht, die Herzfrequenz dann allerdings mit zunehmender Dosis (nicht linear) abnimmt und dann ab einer gewissen Dosis wieder (nicht-linear) zunimmt.
Fall d) Hier lässt sich ebenfalls ein deutlicher Zusammenhang erkennen, dieser ist aber auch komplexer als in den Fällen a) und b). Hier steigt die Herzfrequenz zwar zunächst mit der Dosis, ab einer bestimmten Dosis verringert sich dann jedoch die Herzfrequenz mit zunehmender Dosis.
Fall e) Hier lässt sich kein Zusammenhang erkennen. Unabhängig von der Dosis bleibt die Herzfrequenz im Großen und Ganzen konstant.
Fall f) Hier lässt sich kein Zusammenhang erkennen. Die Punkte scheinen vollkommen zufällig verteilt zu sein.
Die Sache mit der Korrelationsanalyse ist nun, dass Zusammenhänge wie in Fall c) und d) dargestellt, nicht von der Korrelation „erfasst“ werden. Heißt: Man sieht sofort, dass ein ziemlich eindeutiger Zusammenhang vorliegt, berechnet man jedoch die Korrelation, dann wäre diese in etwa so hoch wie in den Fällen e) und f), bei denen kein Zusammenhang vorliegt.
Daher unbedingt merken:
- Mit der Korrelation erfasst man nur den linearen Zusammenhang zwischen zwei Merkmalen. Vereinfacht gesagt heißt „linear“ dabei, dass man, wie du in Fall a) und b) sehen kannst, die Punktwolke gut durch eine Gerade repräsentieren kann, die einen positiven (wie in Fall a) oder negativen (wie in Fall b) Anstieg hat. Liegt ein anderer Typ von Zusammenhang vor (wie in Fall c und d), dann ist die Berechnung der Korrelation nicht sinnvoll.
- Daher solltest du dir bei der Analyse von Zusammenhängen zwischen zwei Merkmalen als ersten Schritt deine Daten immer grafisch veranschaulichen, um beurteilen zu können, ob die Berechnung der Korrelation überhaupt sinnvoll ist.
Nachdem wir diesen wichtigen Punkt geklärt haben, werden wir uns nun anschauen, welche Werte die Korrelation überhaupt annehmen kann und wie die Größe der Korrelation mit der „Form“ der zugehörigen Punktwolke zusammenhängt.
Interpretation der Korrelation
Angenommen, du hast dir also nun deine Daten grafisch veranschaulicht und die Berechnung der Korrelation ist tatsächlich sinnvoll (heißt: es liegt kein nicht-linearer Zusammenhang vor). Was bedeutet dann die Größe der Korrelation?
Die Korrelation soll die Stärke des linearen Zusammenhangs in einer Zahl ausdrücken. Daher wäre es nützlich, wenn
- die Korrelation den Wert 0 annimmt, wenn kein linearer Zusammenhang vorliegt,
- die Korrelation umso größer wird, je größer der lineare Zusammenhang ist
- du anhand der Korrelation sehen kannst, ob ein positiver linearer Zusammenhang („je mehr von dem einen, desto mehr auch von dem anderen“) oder ein negativer linearer Zusammenhang („je mehr von dem einen, desto weniger von dem anderen“) vorliegt, und
- die Größe der Korrelation unabhängig von Einheit, Mittelwert und Standardabweichung der beiden Variablen wäre, sodass die Interpretation der Größe der Korrelation für jede mögliche Untersuchungssituation immer die gleiche ist und du somit auch Korrelationen aus unterschiedlichen Studien miteinander vergleichen kannst.
Glücklicherweise erfüllt die Korrelation all diese Eigenschaften! Danke, Statistik! 😉
Normierung des Korrelationskoeffizienten
Berechnest du die Korrelation, dann liegt diese immer im Bereich zwischen -1 und +1. Das Vorzeichen gibt dir dabei an, ob ein positiver (+) oder ein negativer (-) linearer Zusammenhang zwischen den beiden Merkmalen vorliegt. Ist die Korrelation 0, liegt kein linearer Zusammenhang vor. Je näher die Korrelation bei den beiden „Endpunkten“ +1 bzw. -1 liegt, umso „stärker“ ist auch der positive bzw. negative lineare Zusammenhang zwischen beiden Variablen. Ist die Korrelation genau +1 oder -1, dann liegen sämtliche Punkte der Punktwolke auf einer Geraden (mit positivem oder negativem Anstieg).
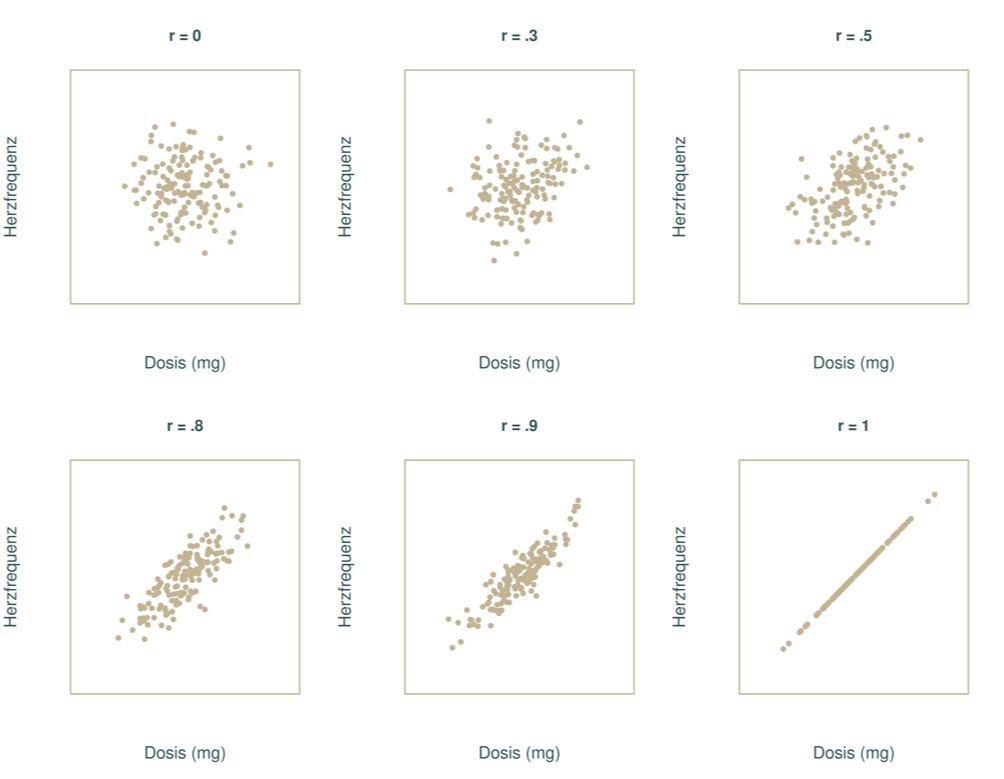
In den folgenden Grafiken kannst du einen Eindruck davon bekommen, wie für verschiedene mögliche „Punktwolkenformen“ die zugehörige Größe der Korrelation aussieht.
Die Korrelation zwischen zwei Variablen wird in der Statistik auch kurz mit r bezeichnet und steht hier über der jeweiligen Punktwolke.
Wir beginnen mit Beispielen für die positive Korrelation:
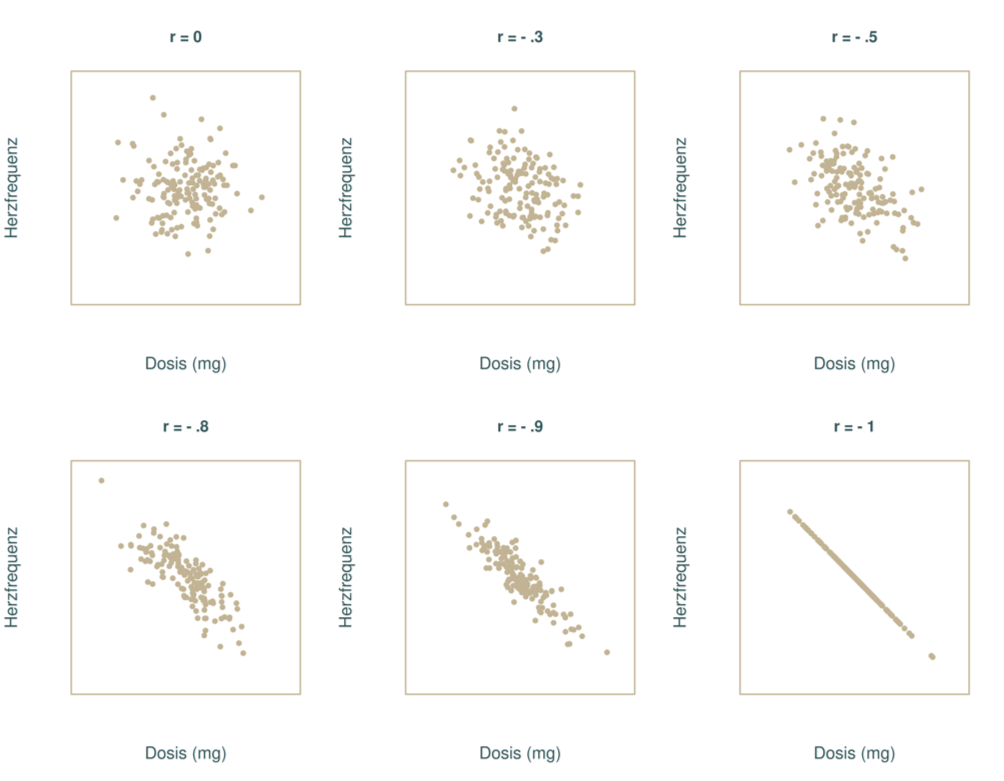
Und hier das Gleiche noch einmal für die negative Korrelation:
Man kann hier wunderbar sehen, dass mit zunehmender Größe der Korrelation die Form der Punktwolke immer „schmaler“ wird und sich immer weiter einer Geraden annähert.
Bei einer Korrelation von +1 oder -1, also wenn alle Punkte auf einer Geraden liegen, spricht man auch von einem „perfekten linearen Zusammenhang“ oder auch von einem „deterministischen Zusammenhang“. Dieser Fall wird natürlich in Praxis so gut wie nie auftreten (und bei Patientendaten schon dreimal nicht).
Zur weiteren Interpretation der Größe der Korrelation greift man häufig auf eine Konvention von Cohen (1988) zurück, nach der es sich bei Korrelationen von
- .1 ≤ |r| < .3 um „kleine Zusammenhänge“
- .3 ≤ |r| < .5 um „mittlere Zusammenhänge“ und
- |r| > .5 um „große Zusammenhänge“
handelt (|r| steht hier für die absolute Größe der Korrelation, also unabhängig vom Vorzeichen).
WICHTIG: Eine Korrelation von 0 oder nahe 0 bedeutet NICHT zwangsläufig, dass kein Zusammenhang zwischen den beiden Merkmalen besteht, sondern eben nur, dass kein linearer Zusammenhang besteht. Würdest du etwa die Korrelation von Fall c) von oben berechnen, dann würdest du eine Korrelation von fast 0 (r = – 0.0034, wenn du es genau wissen möchtest) bekommen, obwohl ein nahezu perfekter, aber eben nicht-linearer, Zusammenhang zwischen Dosis und Herzfrequenz besteht!
Um diesen Punkt nochmal anschaulich zu verdeutlichen zeigt die folgende Graphik wieder die Punktwolke von Fall c), diesmal ist zusätzlich die zugehörige Regressionsgerade eingezeichnet.

Das Thema dieses Artikels ist zwar die Korrelation, aber es besteht ein enger inhaltlicher Zusammenhang zwischen der Korrelation und der einfachen linearen Regression. Ganz einfach gesprochen lässt sich anhand des Anstiegs der Regressionsgeraden die „Richtung“ der Korrelation ablesen. Liegt eine positive Korrelation vor, ist auch der Anstieg der Regressionsgeraden positiv. Liegt hingegen eine negative Korrelation vor, ist auch der Anstieg der Regressionsgeraden negativ. Bei einer Korrelation von 0 hat die Regressionsgerade einen Anstieg von 0, ist also einfach nur eine „waagerechte Linie“, wie es hier in Fall c) vorliegt.
Außerdem solltest du bei der Interpretation deiner Korrelation auch nicht in die folgenden Fallen stolpern…
Stolperfallen bei der Interpretation
1. Korrelation vs. Kausalität
Dass Korrelation und Kausalität zwei verschiedene Paar Schuhe sind hast du vermutlich schon einmal gehört. Die Korrelation ist erst einmal nichts anderes als eine formal-statistische Eigenschaft zwischen zwei Variablen und sagt für sich genommen überhaupt nichts über irgendwelche möglichen Ursache-Wirkungszusammenhänge aus.
Beispielsweise wurde in ziemlich vielen (und ziemlich oft zitierten) Studien eine positive Korrelation zwischen dem Spielen von Ego-Shootern und der Aggressionsbereitschaft gefunden. Aber heißt das nun, dass das vermehrte Spielen von Ballerspielen die höhere Aggressionsbereitschaft kausal verursacht? Und sollte man deshalb nicht besser alle Ballerspiele verbieten?
Diese Frage ist schwer zu beantworten, aber sie lässt sich definitiv nicht allein über Korrelationsanalysen beantworten. Es ist natürlich möglich, dass das Spielen von Ballerspielen die Aggressionsbereitschaft erhöht. Ebenso möglich ist es allerdings auch, dass Personen mit erhöhter Aggressionsbereitschaft eben gerne Ballerspiele spielen. Und es kann natürlich auch sein, dass ein oder mehrere andere Faktoren (z.B. genetische Dispositionen) sowohl die erhöhte Aggressionsbereitschaft als auch die Liebe zu Ballerspielen verursacht.
Es gibt selbstverständlich auch Fälle, bei denen bestimmte Möglichkeiten von vornherein unplausibel sind. In unserem Beispiel ist es etwa ziemlich unplausibel, dass eine erhöhte Herzfrequenz eine höhere Medikamentendosis „verursacht“.
Als Faustregel kannst du dir aber merken: Du solltest generell die Korrelation zwischen zwei Merkmalen für sich allein genommen nicht kausal interpretieren.
2. Scheinkorrelationen
Häufig findet man auch substanzielle Korrelationen zwischen Merkmalen, die in keinerlei (theoretischem) Bezug zueinanderstehen. So lässt sich etwa ein fast perfekter linearer Zusammenhang (r = .996) zwischen der Scheidungsrate in Maine (Bundesstaat in den USA) und dem Margarinekonsum pro Kopf in den USA feststellen. Ein Fall für die nächste Ausgabe von Science? Besser nicht…
Solche Korrelationen bezeichnet man auch als Scheinkorrelationen. Der Punkt dabei ist, dass man alles Mögliche miteinander korrelieren kann und dann eben hin und wieder auch durchaus substanzielle Korrelationen findet, die aber auf inhaltlich-theoretischer Ebene vollkommen bedeutungslos oder „zufällig“ sind.
Für dich heißt das: Du solltest in deinen Daten nicht einfach alle möglichen Korrelationen berechnen (nur weil die lediglich einen Klick entfernt sind und du es kannst), sondern wie auch bei allen anderen statistischen Analysen immer theoriegeleitet vorgehen. Das heißt, du solltest aufgrund klinisch-theoretischer Überlegungen begründete Vermutungen haben, warum bestimmte Merkmale in einem Zusammenhang stehen sollen.
Eine wirklich nette Zusammenstellung wirklich lustiger Scheinkorrelationen lässt sich übrigens unter
https://www.tylervigen.com/spurious-correlations
finden.
3. Verdeckte Korrelationen/Simpson-Paradox
Ein weiterer Punkt, den du bei Korrelationsanalysen stets beachten solltest, ist, dass deine berechnete Korrelation nicht „absolut“ zu verstehen ist. Was ist damit gemeint? Das lässt sich am besten wieder anhand eines einfachen Beispiels erklären, das auch als „Simpson-Paradox“ bekannt ist (obwohl es sich genau genommen gar nicht um ein Paradoxon handelt, aber es klingt halt toll).
Nehmen wir mal an, du hättest für unser Beispiel von oben (Medikamentendosis und Herzfrequenz) folgende Punktwolke bekommen (zur Verdeutlichung ist auch hier wieder die zugehörige Regressionsgerade eingezeichnet):

Berechnest du jetzt für diese Daten die Korrelation zwischen Medikamentendosis und Herzfrequenz, dann ist diese hier r = – 0.54. Es besteht also ein recht großer negativer linearer Zusammenhang, was du auch an dem negativen Anstieg der Regressionsgerade ablesen kannst.
Nehmen wir weiter an, du würdest jetzt die Männer und die Frauen deiner Stichprobe (farblich) getrennt betrachten und bekämst dann folgende Punktwolke:
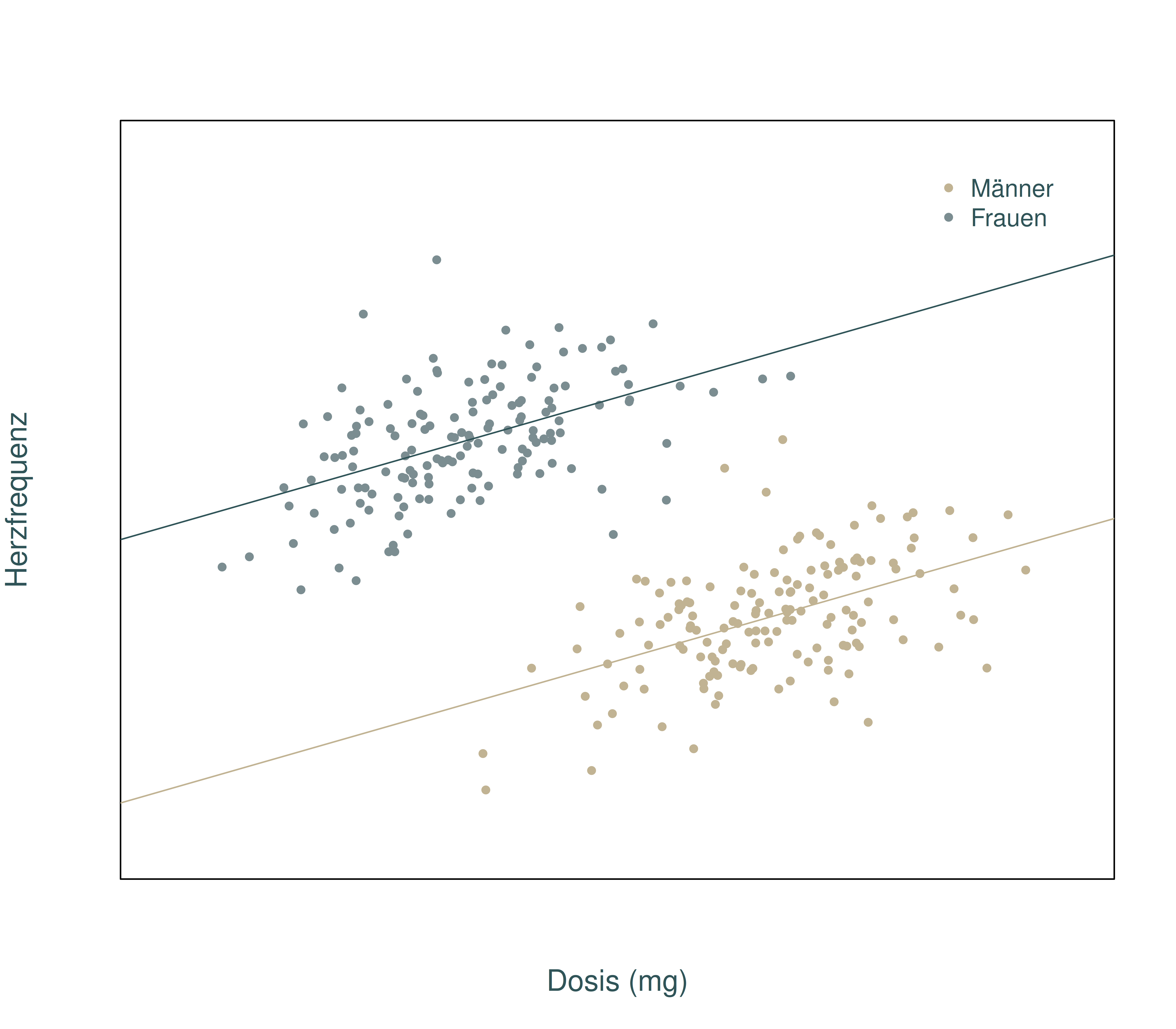
Beachte, dass die Datenpunkte bei beiden Punktwolken vollkommen identisch sind! Würdest du jetzt aber die Korrelation zwischen Dosis und Herzfrequenz für die Männer und Frauen getrennt berechnen, dann wäre die sowohl für die Männer als auch für die Frauen in etwa r = 0.6, also jeweils ein recht großer positiver linearer Zusammenhang! Dass es sich hier um jeweils positive lineare Zusammenhänge handelt kannst du wiederum an den beiden Regressionsgeraden ablesen, die hier für die Frauen und die Männer getrennt eingezeichnet sind.
Was soll dir dieses Beispiel zeigen? Wenn du Korrelationsanalysen durchführst, dann ist das Ergebnis immer von deiner konkreten „Datenkonstellation“ abhängig, und zwar insbesondere von weiteren Variablen, die du in deine Analyse(n) mit einbeziehst (in dem Beispiel das Geschlecht).
Das Problem ist allerdings, dass du bei der Datenerhebung natürlich gar nicht vollständig wissen kannst, welche Variablen für die Analyse wichtig sein könnten. So könnte etwa in unserem Beispiel der lineare Zusammenhang zwischen Dosis und Herzfrequenz wieder anders aussehen, wenn man jetzt noch zusätzlich getrennt nach sozioökonomischem Status, Vorliegen einer bestimmten Krankheit, BMI usw. auswerten würde.
Du siehst also, die eigentliche Schwierigkeit bei Zusammenhangsanalysen besteht nicht darin, diese durchzuführen (das macht ein Programm für dich), sondern die Ergebnisse klinisch-inhaltlich angemessen zu interpretieren!
Und dafür ist auch (wieder mal) der Unterschied zwischen Stichprobe und Population wichtig!
Stichprobe und Population
Bisher haben wir ja nur darüber gesprochen, wie man für eine konkrete Stichprobe die Korrelation berechnet. In der Regel möchtest du aber nicht (nur) wissen, ob ein linearer Zusammenhang zwischen zwei Merkmalen deiner Stichprobe besteht, sondern ob ein solcher Zusammenhang in der Population, aus der deine Stichprobe stammt, existiert. Oder kurz gesagt: Du möchtest einen inferenzstatistischen Test durchführen.
In unserem Beispiel möchtest du also nicht nur wissen, ob sich ein Zusammenhang zwischen Medikamentendosis und Herzfrequenz bei den 100 von dir untersuchten Personen finden lässt, sondern eben ganz allgemein, auf alle Personen bezogen.
Glücklicherweise folgt auch der Korrelationstest der üblichen Logik inferenzstatistischer Tests, die du in unserem Grundlagenartikel dazu nachlesen kannst.
Die Korrelation auf Populationsebene wird mit ρ (sprich: rho) bezeichnet und die Null- und Alternativhypothese für diesen Test lauten demzufolge:
H0: ρ = 0
H1: ρ ≠0
Die H0 besagt also, dass auf Populationsebene kein linearer Zusammenhang besteht und die (ungerichtete) H1 besagt, dass ein linearer Zusammenhang besteht, wobei nicht spezifiziert ist, ob dieser positiv oder negativ ist. Gelegentlich findet man auch Situationen, in denen die H1 gerichtet ist, also spezifisch auf einen positiven bzw. negativen linearen Zusammenhang getestet wird.
Als Ergebnis deines Tests bekommst du wieder einen p-Wert und wenn dieser kleiner ist als dein α, dann solltest du die H0 verwerfen. Und hier gilt natürlich auch wieder, dass der p-Wert von der Stichprobengröße beeinflusst wird und du dein Ergebnis auf den 3 Ebenen statistische Signifikanz, Effektgröße und klinische Bedeutsamkeit interpretieren solltest. Falls dir das alles nichts sagt: Das alles ist ausführlich in unserem Grundlagenartikel erklärt!
Was du tun kannst, wenn deine beiden Variablen nicht intervallskaliert sind, erklären wir dir nun im letzten Abschnitt.
Spezialfälle der Korrelation
Wenn deine beiden Merkmale nicht intervallskaliert sind, dann lassen sich glücklicherweise trotzdem Zusammenhangsanalysen durchführen, in denen nicht die Produkt-Moment-Korrelation, sondern eine andere „Korrelationsvariante“ berechnet werden kann. Ohne näher darauf einzugehen, wie genau diese verschiedenen Varianten berechnet werden, wollen wir dir hier eher einen Überblick anbieten.
1. Fall: Eine intervallskalierte und eine ordinalskalierte Variable oder zwei ordinalskalierte Variablen
Für diesen Fall lässt sich die Rangkorrelation, auch Spearman-Korrelation genannt, berechnen. Auch diese liegt immer zwischen – 1 und +1 und lässt sich prinzipiell so interpretieren wie die Produkt-Moment-Korrelation.
Die Spearman-Korrelation ist mit Abstand der am häufigsten auftretende „Spezialfall“ und nach der Produkt-Moment-Korrelation die am zweithäufigsten verwendete Art der Korrelationsanalyse.
2. Fall: Eine intervallskalierte Variable und eine dichotome Variable
Hier lässt sich die punktbiseriale Korrelation berechnen, auch diese liegt immer zwischen -1 und +1. Die Interpretation hängt hier davon ab, welche Ausprägung der dichotomen Variable mit ‚0‘ und welche mit ‚1‘ kodiert ist. Eine positive punktbiseriale Korrelation bedeutet dabei, dass ein positiver Zusammenhang zwischen der intervallskalierten Variable und der Ausprägung der dichotomen Variable, die mit ‚1‘ kodiert ist, vorliegt. Wurde beispielsweise das Geschlecht (0 = Männer, 1 = Frauen) und die Herzfrequenz erhoben und du bekommst eine positive punktbiseriale Korrelation, dann bedeutet das inhaltlich, dass die Frauen deiner Stichprobe eine höhere Herzfrequenz aufweisen als die Männer (und bei einer negativen Korrelation genau andersherum).
Gelegentlich gibt es auch Situationen, in denen eine intervallskalierte Variable künstlich dichotomisiert wird. So könnte man etwa das Alter von Patienten lediglich in 2 Kategorien („jung“ und „alt“) einteilen. Für diesen Spezialfall (eine intervallskalierte und eine künstlich dichotomisierte Variable) lässt sich auch die biseriale Korrelation berechnen.
Die biseriale Korrelation kann auch Werte außerhalb des Bereiches zwischen -1 und +1 annehmen. Zusätzlich ist die Berechnung nur dann sinnvoll, wenn die beiden intervallskalierten Variablen normalverteilt sind. Im Zweifel solltest du daher stets die punktbiseriale Korrelation vorziehen.
3. Fall: Eine ordinalskalierte Variable und eine dichotome Variable
In diesem Fall lässt sich die biseriale Rangkorrelation berechnen. Der Wertebereich ist hier wieder zwischen -1 und +1 und die Interpretation analog zur punktbiserialen/biserialen Korrelation.
4. Fall: Zwei dichotome Variablen
Hast du zwei dichotome Variablen, dann kannst du den Φ-Koeffizienten (sprich: phi) oder Cramérs V bestimmen. Beide Größen sind ist eng verwandt mit dem Kontingenzkoeffizienten χ2 (sprich: Chi2), der sich allgemein für zwei kategoriale/qualitative Variablen berechnen lässt. Der Φ-Koeffizient kann auch Werte außerhalb des Bereiches zwischen -1 und +1 annehmen und die Interpretation des Koeffizienten hängt hier wesentlich von der Kodierung der beiden dichotomen Variablen ab.
Möchtest du den Φ–Koeffizienten oder Cramérs V im Rahmen des χ2-Tests berechnen, haben wir hier einen Onlinekurs zum Thema erstellt.
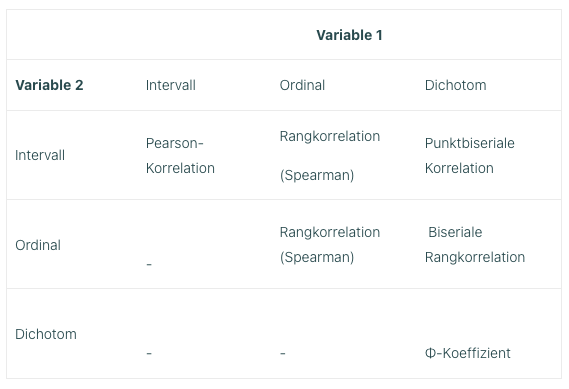
Wir haben dir zum besseren Überblick die verschiedenen Korrelationsarten bei unterschiedlichen Skalentypen der beiden Variablen in folgender Tabelle noch einmal zusammengefasst.
|
Variable 1 |
|||
| Variable 2 | Intervall | Ordinal | Dichotom |
| Intervall | Pearson-Korrelation |
Rangkorrelation |
Punktbiseriale Korrelation |
| Ordinal |
– |
Rangkorrelation (Spearman) | Biseriale Rangkorrelation |
| Dichotom |
– |
– |
Φ-Koeffizient |
Da die Berechnung einer Korrelation (egal welche) wirklich nur einen Klick erfordert und du aber durch simples Anklicken und Berechnen leider auch schnell in eine der dargestellten Stolperfallen taumeln kannst, solltest du, wenn du Zusammenhangsanalysen durchführst, bestenfalls immer nach dem folgenden Schema vorgehen:
- Überlege dir vorher, welche inhaltlich-theoretischen Vermutungen du bzgl. des Zusammenhangs zwischen den beiden Merkmalen hast und warum du diese hast! Gibt es vielleicht noch eine Variable, die du zusätzlich mit in deine Analysen einbeziehen solltest (siehe Simpson-Paradox)?
- Veranschauliche dir deine Daten in einer Grafik (ja, unbedingt)!
- Überlege anhand der graphischen Veranschaulichung deiner Daten, ob die Berechnung einer Korrelation überhaupt für deinen Fall sinnvoll ist!
- Berechne die Korrelation und führe ggf. einen statistischen Test durch!
- Interpretiere die Korrelation und das Testergebnis auf den 3 Ebenen statistische Signifikanz, Effektgröße und inhaltlich-klinische Bedeutsamkeit!
Nicht-lineare Zusammenhänge analysieren
Falls du bei der graphischen Veranschaulichung deiner Daten feststellen solltest, dass bei dir ein nicht-linearer Zusammenhang (z.B. ein quadratischer wie in Fall c) von oben) vorliegt, dann solltest du natürlich die Korrelation nicht berechnen (weder die Korrelation nach Pearson noch die nach Spearman)! Aber was kannst du in diesem Fall alternativ verwenden, um die Größe des Zusammenhangs zwischen deinen beiden Variablen zu beschreiben?
Hier kommt es ein wenig darauf an, was das genaue Ziel deiner Untersuchung ist. Möchtest du die Daten eher in einem Regressionskontext analysieren, dann könntest du auf nichtlineare oder polynomiale Regressionen zurückgreifen. Beides sind recht komplexe Verfahren, die wir dir an anderer Stelle erklären. Wenn du allerdings „lediglich“ die Stärke des Zusammenhangs zwischen deinen beiden Variablen erfassen und inferenzstatistisch testen möchtest, dann ist die sog. Distanzkorrelation (distance correlation) die Methode der Wahl! Das ist ein recht neues und im Vergleich zur „normalen Korrelation“ mathematisch deutlich anspruchsvolleres Konzept, das sich aber generell auf jede „Art“ von Zusammenhang (selbst lineare) anwenden lässt. Eine einfache Berechnung der Distanzkorrelation in SPSS ist bisher nicht möglich, in R hingegen lässt sich die Distanzkorrelation über einen einfachen Befehl berechnen. Vielleicht also ein weiterer Grund, sich näher mit R auseinanderzusetzen… 😉
Wie R funktioniert erklären wir dir übrigens ebenfalls in unserem Grundlagenkurs.
Und ganz zum Schluss noch ein kurzer Ausblick: Die Korrelation (Pearson-Korrelation) zwischen zwei Variablen wird uns im Kontext der einfachen linearen Regression wieder begegnen und dort eine zentrale Rolle spielen. Die Regressionsgerade soll ja gerade den linearen Zusammenhang zwischen der abhängigen Variable und dem Prädiktor widerspiegeln und „wie gut“ die Regressionsgerade deine Daten beschreibt ist dann letztendlich von der (absoluten) Größe der Korrelation zwischen abhängiger Variable und Prädiktor abhängig.
Freu dich also schon, auf das, was kommt und leg bis dahin schon einmal mit der Berechnung deiner Korrelation los!
Viel Spaß!