Wie interpretiere ich eine ANOVA?
In diesem Artikel erkläre ich dir, wie du die Effekte einer ANOVA interpretierst und welche Arten von ANOVAs es gibt.
Die ANOVA ist eines der am häufigsten verwendeten statistischen Verfahren in der Medizin.
Sie ist sehr effektiv und erspart dir eine Menge Probleme, sobald du mehr als zwei Gruppen oder zwei Zeitpunkte miteinander vergleichen möchtest.
In dieser Artikelreihe erkläre ich dir deshalb wie ANOVAs funktionieren, welche Effekte es innerhalb der ANOVA gibt und welche 3 Typen der ANOVA du kennen solltest.
In diesem ersten Artikel stelle ich dir das allgemeine Konzept hinter der ANOVA vor und welche Effekttypen sie umfasst. Eine ANOVA korrekt zu berechnen und zu interpretieren, ist ohne dieses Wissen nicht möglich. Daher ist es wichtig, dass du diesen Artikel zuerst liest.
Hast du die Effekte der ANOVA verstanden, kannst du im nächsten Schritt überlegen, welcher ANOVA-Typ der richtige für dich ist und in den ANOVA-spezifischen Artikeln nachlesen, wie du ihn korrekt durchrechnest.
Die Grundlagen der ANOVA
Innerhalb der ANOVA testest du den Einfluss einer oder mehrerer nominaler Variablen auf eine metrische Variable.
Wir schauen also z. B., ob Variablen wie die gegebene Schmerzmittel eines Patienten (nominal) einen Einfluss auf sein Schmerzempfinden (metrisch) hat.
Du siehst sicher schon, dass diese nominale Variable relativ gut in Klassen einteilbar ist. Man hat also entweder Paracetamol oder Ibuprofen bekommen. Zwischenformen gibt es nicht. Somit gehören Patienten in innerhalb der ANOVA entweder der einen oder anderen Gruppe an. Und der Einfluss dieser Gruppe wird dann geprüft.
Die Gruppenvariable nennen wir im Rahmen der ANOVA auch Faktor (in diesem Fall: die Diagnose). Die einzelnen Ausprägungen des Faktors (Paracetamol vs. Ibuprofen) nennen wir Faktorstufen. Und weil nur wir die Faktorstufen innerhalb unserer Studie beliebig manipulieren können, nennt man den Faktor auch die unabhängige Variable.
Im Gegenzug dazu gibt es innerhalb der ANOVA die abhängige Variable. Sie ist die Variable, bei der wir einen Effekt erwarten, sobald wir die Ausprägungen der unabhängigen Variable(n) verändern.
Wir geben also Paracetamol oder Ibuprofen und schauen dann, wie sich das auf das Schmerzempfinden auswirkt.
Im Fall der ANOVA ist die abhängige Variable metrisch skaliert. Metrische Variablen sind gleichmäßig skaliert, d. h. alle Einheiten haben den gleichen Abstand zueinander (1 cm ist genauso weit von 2 cm entfernt, wie 77 von 78 cm). Typische metrische Variablen sind das Alter, das Gewicht oder die Körpergröße.
Fazit:
Im Rahmen der ANOVA prüfen wir also, wie sich die Effekte einer nominal skalierten Variablen auf eine metrisch skalierte Variable auswirken.

Flowchart
ANOVA für Gruppenvergleiche
Das Design der ANOVA
„Aber ist das nicht genau das Gleiche wie beim t-Test?“
Ja und nein. Das Tolle an der ANOVA ist nämlich, dass du anders als bei einem t-Test nicht nur zwei Gruppen miteinander vergleichen kannst, sondern auch 3 oder 4, oder soviele du willst.
Aber es kommt noch besser: Die ANOVA erlaubt dir nicht nur den Einfluss eines Faktors zu testen, sondern mehrerer!
Ihre Ergebnisse zeigen dir also nicht nur den Effekt eines einzelnen Faktors an (wie z.B. der t-Test) , sondern auch die Effekte mehrerer Faktoren oder sogar deren Kombinationen! Das meine ich mit effektiv!
Du könntest also testen, ob die Wirkdauer des Schmerzmittels A oder B davon abhängig ist, wie hoch die verabreichte Dosis war (auch hier wieder nominalskaliert als niedrige, mittlere und hohe Dosis).
Das ist praktisch, denn anders als in einem einfachen t-Test, der dir nur den Vergleich eines Faktors mit zwei Stufen erlaubt (= den Vergleich zweier Gruppen), kannst du innerhalb der ANOVA recht komplexe Effektstrukturen aufbauen, indem du mehrere Faktoren mit vielen Faktorstufen kombinierst.
Hier siehst du unser Beispiel – die Kombination der Faktoren Schmerzmittel und Dosis:


Allerdings – und das siehst du wahrscheinlich auch sofort – resultiert die Kombination verschiedener Faktoren in sehr vielen Untergruppen, in diesem Fall 6, die du alle mit ausreichend vielen Patienten füllen musst, damit die ANOVA sinnvolle Ergebnisse liefern kann.
Das ist Nachteil hat die ANOVA: Du musst genauso viele Untergruppen mit Patienten befüllen, wie sich aus der Kombination der einzelnen Faktoren samt ihrer Faktorstufen ergibt. Es ist nicht möglich, Untergruppen leer zu lassen!
Daher rate ich dir während deiner Studienplanung darauf zu achten, nicht mehr als zwei Faktoren mit nicht mehr als 4 Unterstufen im stufenreichsten Faktor einzuplanen. Allein diese Kombination würde schon in mindestens 8 Untergruppen resultieren, für die du ausreichend viele Patienten rekrutieren müsstest. Je komplexer dein Design also ist, desto schwieriger wird es.
Die Effekte der ANOVA
In unserer Beispiel-ANOVA testest du 2 Faktoren, die in insgesamt 3 Effekten resultieren:
1. dem Haupteffekt „Schmerzmittel“:
Unterscheiden sich beide Schmerzmittel bzgl. ihrer Wirkdauer, ganz unabhängig davon, welche Dosis gegeben wurde.
2. dem Haupteffekt „Dosis“:
Unterscheidet sich die Wirkdauer zwischen den 3 gegeben Dosierungen, ganz unabhängig von dem gegebenen Schmerzmittel.
3. der Interaktion „Schmerzmittel x Dosis“:
Unterscheidet sich die Wirkdauer zwischen den verschiedenen Dosierungen in Abhängigkeit vom gegebenen Schmerzmittel?
Du siehst also es gibt Haupteffekte, die den Effekt eines jeden Faktors einzeln betrachten, ganz unabhängig von Ausprägungen des anderen Faktors.
Der Haupteffekt „Schmerzmittel“ zeigt dir also, ob sich die Wirkdauer von Ibuprofen und Paracetamol generell unterscheidet – ob die Dosis dabei hoch, mittel oder niedrig war, wird nicht berücksichtigt.
Genauso ist es auch beim Haupteffekt Dosis, hier wird nur ganz allgemein getestet, ob wie sich die gegebene Dosis auf die Wirkdauer auswirkt, welches Medikament gegeben wurde, ist dabei irrelevant.
Aber wollten wir nicht eigentlich wissen, ob die Kombination beider Faktoren einen wichtigen Einfluss auf die Wirkdauer hat?
Ganz genau. Richtig interessant wird es erst, wenn wir prüfen, ob sich die Wirkdauer zwischen den drei Dosierungen je nach Schmerzmittel unterscheiden.
Und genau das ist unser Interaktionseffekt.
Er zeigt dir an, ob die Kombination aus beiden Faktoren einen systematischen Effekt auf deine abhängige Variable hat. Und das wollen wir ja wissen – sonst hätten wir uns die Mühe mit den verschiedenen Faktoren ja nicht gemacht. Die Haupteffekte sind somit oft Beiwerk, das wir interpretieren, wenn die Interaktion nicht signifikant geworden ist.
Aber was heißt das eigentlich, wenn Haupteffekte oder Interaktionen signifikant werden?
Prinzipiell alles und nichts. Das Besondere an der ANOVA ist nämlich, dass sie ein übergeordneter Test ist. Ihre Effekte sagen uns nur, DASS da irgendwo innerhalb der Haupt- bzw. Interaktionseffekte systematische Unterschiede zwischen den Gruppen versteckt sind, sie sagen uns aber nicht WO.
Signifikante Haupteffekte bzw. Interaktionen geben uns somit zuerst einmal die Erlaubnis, dort, wo die Signifikanz aufgetreten ist, genauer nachzuschauen, wo die Effekte genau liegen. Und zwar mit Hilfe von direkten Vergleichen in Form von t-Tests oder aber über geplante Kontraste – je nachdem, ob du vorab Hypothesen definiert hast und welches Verfahren dir lieber ist.
Wichtig dabei zu wissen ist, dass du im Falle einer signifikanten Interaktion weitere signifikante Haupteffekte ignorieren kannst. Das liegt daran, dass eine signifikante Interaktion darauf hindeutet, dass sich der wirklich bedeutsame Effekt nur in manchen Faktorstufenkombinationen abspielt, in anderen aber nicht. Das könnte z.B. der Fall sein, wenn die Wirkdauer nur bei einem der beiden gegebenen Schmerzmittel mit höherer Dosis stetig ansteigt, bei dem anderen Medikament aber nicht.
Interpretierst du also trotz einer signifikanten Interaktion den Haupteffekt Dosis, weil sich der Effekt des einen Schmerzmittels in diesem „Gemisch“ beider Schmerzmittel durchsetzt, dann erliegst du fälschlicherweise dem Eindruck, dass eine höhere Dosis immer eine längere Wirkdauer zur Folge hat, egal welches Medikament gegeben wurde. Und das ist natürlich verkehrt und würde zu völlig falschen Therapieempfehlungen führen.
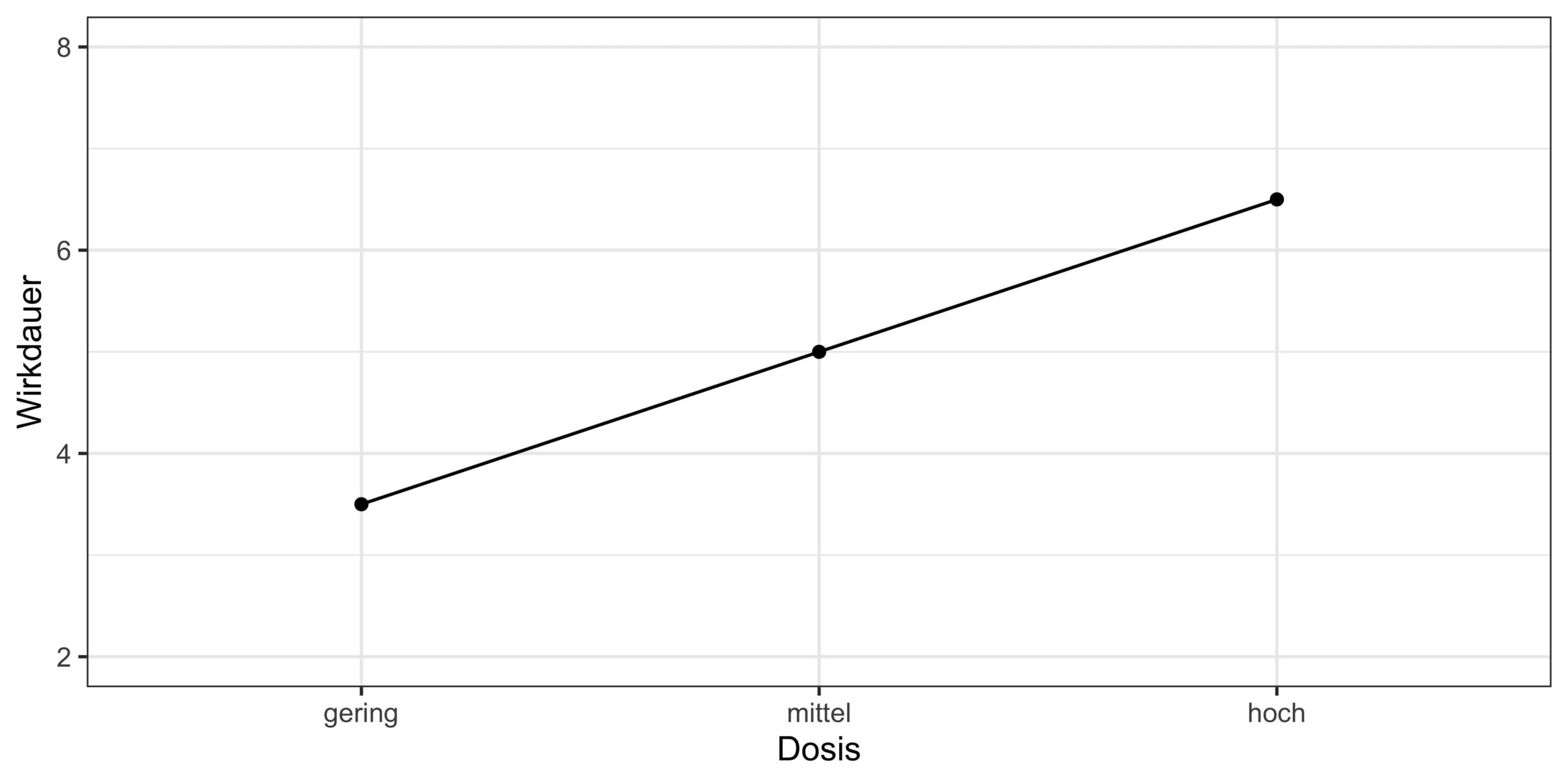
In diesen Grafiken wird das noch mal deutlich:
Abb. 1. Interaktion Schmerzmittel x Dosis: Sie zeigt dir, dass nur Ibuprofen einen Dosiseffekt hat (höhere Dosis = längere Wirkdauer), Paracetamol dagegen nicht (die Wirkdauer ist immer gleich lang, egal wie hoch die Dosis war). Das ist natürlich ein ausgedachtes Extrembeispiel und hat nichts mit der wirklichen Wirkdauer beider Mittel zu tun.
Abb. 2. Haupteffekt Dosis: Hier siehst du die gleichen Daten noch einmal, allerdings ohne eine Unterteilung nach Medikament. In diesem Fall mittelt sich der Effekt von Ibuprofen in den Haupteffekt, sodass es so aussieht, als ob es einen generellen Effekt der Dosis gibt, ganz egal welches Medikament gegeben wurde. Das ist natürlich falsch.
Das heißt also (ich wiederhole das lieber mehrfach): Im Falle einer signifikanten Interaktion zweier Faktoren, solltest du unbedingt auf die Interpretation signifikanter Haupteffekte verzichten und dich lieber darauf konzentrieren herauszufinden, worin genau die Effekte der Interaktion begründet sind.
Das machst du mit Hilfe von so genannten Post-hoc-Tests, falls du keine Hypothesen hast, wo die Unterschiede liegen könnten. Hast du genaue, vorab definierte Annahmen kannst du geplante Kontraste verwenden, die du gleich in einem Rutsch im Rahmen der ANOVA mit testest.
Überprüfung der Interaktion anhand ungepaarter T-Tests
Schritt 1:
Um den Einfluss der Dosis auf die Wirkdauer für beide Medikamente einzeln zu testen könntest du ungepaarte T-Tests zwischen der geringen und der mittleren, sowie der mittleren und der hohen Dosis rechnen – allerdings getrennt nach Medikamenten (hierfür benutzt du am besten Filter).
Dort wo du signifikante Ergebnisse in den t-Tests findest liegt dein Effekt. Schau dir für diese Gruppen einfach die Mittelwerte der deskriptiven Statistik an und schon weißt du, wie du die Signifikanzen interpretieren kannst.
Schritt 2:
Um die Unterschiede zwischen den Medikamenten innerhalb jeder einzelnen Dosierung zu testen, vergleichst du die Wirkdauer von Schmerzmittel A und B separat für jede Dosis (auch hier setzt du Filter für die jeweilige Dosierung).
Ist deine Interaktion nicht signifikant, konzentrierst du dich auf die weitere Testung der Haupteffekte. Ist einer von ihnen signifikant, vergleichst du die Faktorstufen des entsprechenden Faktors ebenfalls mit t-Test. In diesem Fall kannst du aber auf das Herausfiltern von Untergruppen des anderen Faktors verzichten.
Möchtest du also den signifikanten Haupteffekt Dosis interpretieren, vergleichst du einfach die drei Dosierungen mit Hilfe von t-Tests untereinander. Ob dabei Paracetamol oder Ibuprofen gegeben wurde, musst du nicht mehr berücksichtigen, da die nicht-signifikante Interaktion dir gezeigt hat, dass der Effekt der Dosierung nicht vom gegebenen Schmerzmittel abhängt.
Noch einfacher wäre es bei einem signifikanten Haupteffekt Medikament. Da hier nur zwei Gruppen zu vergleichen wären müsstest du gar nichts weiter tun, als dir zur Interpretation des Effekts die Mittelwerte der deskriptiven Statistik anzusehen. Das liegt daran, dass ein zweistufiger Haupteffekt vom Prinzip her nichts anderes ist als ein t-Test, auch wenn die Teststatistik eine andere ist.
Ist nur einer der Haupteffekte signifikant, kannst du den anderen einfach ignorieren. Sind beide signifikant, musst du beide interpretieren und nachtesten.
Fazit:
Eine ANOVA interpretierst du immer hierarchisch. Ist die Interaktion signifikant, interpretierst du nur diese anhand von post-hoc Tests. Die Haupteffekte darfst du ignorieren.
Ist die Interaktion nicht signifikant, gehst du „eine Ebene tiefer“ und schaust du dir an, welche der Haupteffekte signifikant sind und differenzierst diese dann anhand weiterer T-Tests aus. Alle nicht signifikanten Haupteffekte können ebenfalls ignoriert werden.
Die Richtung der jeweiligen Untertests kannst du dann anhand von Grafiken oder der deskriptiven Statistik interpretieren.
Vorteile der ANOVA
Nun fragst du dich sicher, warum du denn überhaupt die ANOVA brauchst, wenn du innerhalb der post hoc-Tests trotzdem so viele t-Tests rechnen sollst.
Wie schon erklärt ist die ANOVA ein übergeordnetes Verfahren, ich nenne sie deshalb auch gerne einen globalen Test oder ein Gatekeeper-Verfahren. Diese Namen habe ich mir ausgedacht, aber ich finde sie sehr treffend.
Die ANOVA sondiert für dich vor, ob und wo genau du nach Unterschieden suchen sollst. Ist die Interaktion nicht signifikant, weil sich vielleicht beide Medikamente entlang der Dosierungen ähnlich verhalten (= Haupteffekt Dosierung signifikant), kannst du sofort damit beginnen, die geringe mit der mittleren, und die mittlere mit der hohen Dosis zu vergleichen – und zwar unabhängig von der Gruppe. So hast du dir mit einem Schlag diverse t-Tests gespart und das Risiko von Zufallsbefunden deutlich gesenkt.
Ähnlich verhält sich auch mit deinem zweiten Faktor Schmerzmittel. Ist die Interaktion nicht signifikant, schaust du, ob sich die Medikamente ganz unabhängig von der gegebenen Dosis voneinander unterscheiden.
Das ist zwar ein etwas gröberer Befund, bringt dir aber trotzdem noch einen großen Informationsgewinn.
Sind weder die Interaktion noch die Haupteffekte signifikant, kannst du direkt zur nächsten Hypothese wechseln und das Thema abhaken. Somit sparst du in den allermeisten Fällen sehr viel Zeit. Ganz zu schweigen davon, dass deine Gutachter die ANOVA erwarten, weil sie einfach Standard ist.
Die 3 Arten der ANOVA:
Es gibt 3 verschiedene Typen der ANOVA, die ANOVA für Gruppenvergleiche, die ANOVA für Messwiederholungen und die ANOVA für Gruppevergleiche x Messwiederholungen.
Natürlich haben die in echt etwas kompliziertere Namen, aber ich finde eine bildliche Beschreibung nicht schlecht.
1. Die ANOVA für Gruppenvergleiche:
…wird auch Zwischensubjekt-ANOVA oder Between-Subjects-ANOVA genannt.
Innerhalb der ANOVA für Gruppenvergleiche vergleichen wir verschiedene Patientengruppen miteinander. Wichtig ist dabei, dass jeder Patient nur einer Gruppe angehören kann. Kommt ein Patient mehr als einmal vor, liegt eine Messwiederholung vor und dann ist dies nicht die richtige Art von ANOVA für deine Fragestellung. Ein typisches Beispiel wäre die obige Fragestellung, in der wir die Wirkung verschiedener Medikamente und ggf. verschiedenen Dosierungen auf das Schmerzempfinden prüfen.
2. Die ANOVA für Messwiederholung:
….auch Innersubjekt-ANOVA oder repeated-measures-ANOVA genannt.
Sie benutzt du immer dann, wenn du dieselbe Gruppe von Patienten immer wieder gemessen hast. Ein Beispiel wären Patienten, deren Schmerzscore du in den ersten 3 Tagen post-OP immer wieder erhebst und vergleichst. Auch hier könntest du einen zweiten oder dritten Faktor mit aufnehmen, wenn du z. B. den Effekt EINES Schmerzmittels auf die Schmerzen innerhalb der ersten 3 Tage post-OP erheben wollen würdest und die Patienten jeweils vor und 1h nach der Schmerzmittelgabe fragen würdest, wie hoch ihre Schmerzen sind. Solange du also immer dieselben Patienten mehrfach misst, bist du bei der ANOVA für Messwiederholung richtig.
3. die ANOVA für Messwiederholung x Gruppenvergleiche:
…auch mixed model-ANOVA genannt.
Diesen Typ der ANOVA benutzt du wahrscheinlich am häufigsten. Er wird in der Medizin immer dann verwendet, wenn du verschiedene Gruppen über verschiedene Zeitpunkte immer wieder misst. Ein typisches Beispiel wären Patienten mit derselben Diagnose, die aber unterschiedliche Behandlungen bekommen und deren Behandlungserfolg du nach 1, 2 und 3 Monaten wiederholt erhebst.
Hast du deinen ANOVA-Typ erkannt? Dann lies im nächsten Schritt, wie du die entsprechende ANOVA berechnest.