Aussage über einen vermuteten Zustand der Welt, der am besten anhand der Literatur erarbeitet und untermauert wird.
Es gibt dabei die Alternativhypothese (das ist die Hypothese, die du in deiner Arbeit aufstellst, und in der du formulierst, welchen Effekt du vermutest) und die Nullhypothese (sie beschreibt das Gegenteil zur Alternativhypothese, nämlich, dass es keinen solchen Effekt gibt.)
Inhaltsvalidität liegt dann vor, wenn wir mit einem Instrument inhaltlich tatsächlich das Konstrukt messen, was wir auch messen wollen.
Im Sinne der Fragebogenkonstruktion besteht dann Inhaltsvalidität, wenn das Konstrukt in seiner gesamten Breite unter annähernder Gleichgewichtung aller Teilaspekte abgebildet wird.
Im Gegensatz zur Konstrukt- und Kriteriumsvalidität wird die Inhaltsvalidität für gewöhnlich nicht durch einen numerischen Wert quantifiziert.
Kategoriale Variablen (auch: Nominalskalierte Variable) sind Variablen, deren Ausprägung sich in feste Kategorien einteilen lassen (z. B. die Variable „Haarfarbe“ mit den Ausprägungen „blond“, „braun“, „schwarz“, usw.).
Die Anzahl der möglichen Ausprägungen ist also i. d. R. endlich und jeder Patient sollte nur eine der Ausprägungen einnehmen können.
Eine kategoriale Variable mit zwei möglichen Ausprägungen (z. B. „Lebend“ mit den Ausprägungen „ja“ und „nein“) nennt man auch dichotome Variable.
Konfidenzintervalle geben einen Bereich um einen Punktschätzer an (z. B. um den Mittelwert deiner erhobenen Stichprobe). Sie dienen dazu, uns einen Eindruck darüber zu vermitteln, wie präzise dieser Punktschätzer ist.
Anstatt uns allein auf den Punktschätzer zu konzentrieren und diesen als in Stein gemeißelt anzusehen, berechnen wir stattdessen lieber ein Intervall um den Punktschätzer herum. Dieses Intervall gibt uns einen Eindruck, welchen Wert der „wahre“ Mittelwert der allgemeinen Patientenpopulation mit dem interessierenden Krankheitsbild x denn haben könnte.
Hierfür wählt man häufig das 95%-Konfidenzintervall.
Faustregel: Je schmaler das Konfidenzintervall um den Punktschätzer liegt, desto präziser ist der Punktschätzer selbst.
Aber wie interpretiere ich ein Konfidenzintervall?
Die häufig zu findende Formulierung, dass das berechnete 95%-Konfidenzintervall den gesuchten Parameter mit einer Wahrscheinlichkeit von 95% enthält, ist leider nicht richtig.
Die Interpretation von Konfidenzintervallen ist etwas kniffliger:
Stell dir vor, du stehst vor einer Lostrommel mit 100 Losen und weißt, dass 95 davon „Gewinner“ und 5 „Nieten“ sind. Dann ist die Wahrscheinlichkeit, einen Gewinn zu ziehen, natürlich 95%.
Hast du jetzt aber bereits ein Los gezogen (und schaust es dir noch nicht an), dann ist die Wahrscheinlichkeit für einen Gewinn nicht 95%, sondern entweder 0 (wenn du eine „Niete“ gezogen hast) oder 1 (wenn du einen Gewinn gezogen hast).
Und so ähnlich ist es auch mit den Konfidenzintervallen, die du für deine Stichprobe berechnest:
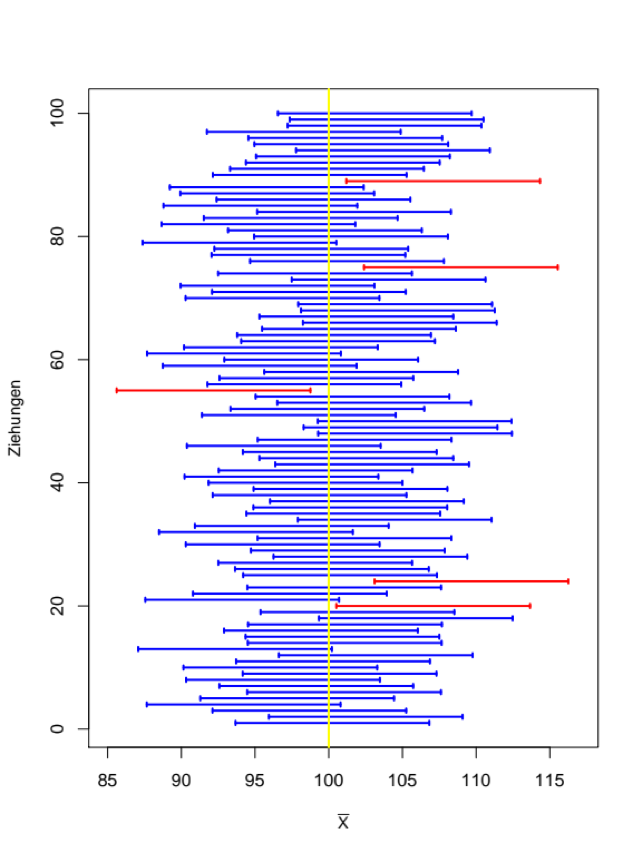
Um dir das einmal bildlich darzustellen, haben wir für dich 100 klinische Stichproben „virtuell“ erhoben und für alle ein Konfidenzintervall um den Mittelwert herum berechnet.
Im Bild siehst du diese Konfidenzintervalle und ihre Position relativ zum „wahren“ Mittelwert der interessierenden Gesamtpopulation (gelbe Linie). Deine Gesamtpopulation wären dabei alle Patienten mit der interessierenden Krankheit x.
Bei 95 der 100 erhobenen klinischen Stichproben überdeckt das berechnete Konfidenzintervall den „wahren“ Mittelwert (blaue Konfidenzintervalle, die die gelbe Linie überdecken). Bei den restlichen 5 Stichproben überdeckt das Konfidenzintervall den wahren Punktschätzer nicht (rote Konfidenzintervalle, die die gelbe Linie nicht überdecken).
Somit liegt VOR der Erhebung deiner Stichprobe die Wahrscheinlichkeit, dass dein später berechnetes Konfidenzintervall den wahren Mittelwert enthält, bei 95%. NACH der Erhebung, wenn du nur eine einzige Stichprobe vorliegen hast, aber bei 0 oder 1, denn der Drops ist ja schon gelutscht (die Stichprobe ist ja schon erhoben).
Was wir aber wissen ist, dass die Wahrscheinlichkeit 95% beträgt, dass wir eine klinische Stichprobe gezogen haben, bei der das zugehörige Konfidenzintervall den gesuchten Parameter enthält. Und das ist ja auch schon was (aber halt ein kleiner konzeptioneller Unterschied, den man im Kopf behalten sollte….Puh..).
Wenn dich das trotzdem noch verwirrt, dann kannst du dir der Einfachheit halber auch weiterhin die Interpretation merken, dass das 95%-Konfidenzintervall den gesuchten Parameter mit einer Wahrscheinlichkeit von 95% enthält. Das wird niemand dran sterben.
Behalte einfach im Hinterkopf, dass das nicht komplett richtig ist.
So berechnest du Konfidenzintervalle:
In SPSS lassen sich Konfidenzintervalle übrigens ganz einfach über Analysieren / Explorative Datenanalyse / Statistiken / Deskriptive Statistik / Konfidenzintervalle (Häkchen setzen) berechnen.
In unseren R-Kursen rechnen wir die Konfidenzintervalle standardmäßig, und völlig automatisch für dich mit. Da musst du dann gar nichts mehr machen.
Die Konfundierende Variable, auch Störvariable genannt, ist eine Variable, welche neben der von uns erhobenen unabhängigen Variable die abhängige Variable beeinflusst (unabhängig davon, ob diese Störvariable erhoben wurde oder nicht).
Eine Möglichkeit Störvariablen „auszuschalten“ wäre es diese mit zu erheben und dann deren Einfluss innerhalb der statistischen Analysen zu kontrollieren (sofern möglich).
Da es aber in der Praxis unmöglich ist, alle Störvariablen zu kennen (geschweige denn zu erheben) empfiehlt es sich in experimentellen Studiendesigns die Zuteilung zu den Experimentalbedingungen randomisiert (also zufällig) vorzunehmen und möglichst große Gruppe zu erheben, da sich Störvariablen bei ausreichend großen Gruppen mit einiger Wahrscheinlichkeit auf alle Experimentalgruppen gleichmäßig verteilen und während der Analyse „rausmitteln“.
Wichtig: Berücksichtigt das Studiendesign nicht die Konfundierung durch mögliche Störvariablen, wird die Datenanalyse und die Diskussion der Studienergebnisse deutlich erschwert! Es ist daher ratsam, viel Zeit in die Studienplanung und Erhebung der Daten zu investieren.
Melde dich für meinen Newsletter an und erhalte sofort das PDF!
Melde dich für meinen Newsletter an und erhalte sofort das PDF!
Melde dich für meinen Newsletter an und erhalte sofort das PDF!
Melde dich für meinen Newsletter an und erhalte sofort die Excel-Vorlage!